| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 리액트네이티브
- GYM
- FirebaseV9
- 클론코딩
- clone coding
- 머신러닝
- 전국국밥
- Reinforcement Learning
- TeachagleMachine
- redux
- selenium
- 딥러닝
- 앱개발
- JavaScript
- pandas
- 사이드프로젝트
- 데이터분석
- ReactNative
- 카트폴
- Instagrame clone
- App
- expo
- kaggle
- React
- python
- coding
- 강화학습
- 강화학습 기초
- 조코딩
- Ros
- Today
- Total
qcoding
[강화학습]A3C_Continuos Actor_Critic_MountainCar 본문
** 이번 실습은 이전 A2C 실습 중 Continuos A2C를 사용했던 것을 A3C로 변경한 것이다. 기본적인 내용은 Continuos A2C 과 동일하며, A3C로 확장할 수 있게 Global Network와 Local Network 구조를 활용하였다.
2023.02.15 - [머신러닝 딥러닝] - [강화학습]Continuos A2C(연속적 A2C)_mountain Car
[강화학습]Continuos A2C(연속적 A2C)_mountain Car
* 이번 실습은 Continuos A2C 실습으로 아래의 Mountain Car Continuos 환경에 연속적 A2C알고리즘을 적용해보는 실습을 하였다. https://www.gymlibrary.dev/environments/classic_control/mountain_car_continuous/ Mountain Car Continu
qcoding.tistory.com
1) 실습에 적용되는 이론

--> 이전 발행글에서 Discreate(이산적)과 Continuos (연속적)인 Action Space에 대하여 설명하였다. Continuos Action의 경우에는 μ (평균), σ (표준편차) 를 인공신경망으로 출력하여 이것을 토대로 정규분포 형태의 Policy를 만들어서 action 선택에 사용한다.
즉, Continuos A2C에서 사용하는 신경망은 아래와 같이 mu (평균) , sigma(표준편차)를 출력으로 사용해서 action을 선택시 이산적인 분포가 아닌 정규분포에서 action을 선택하는 것이 일반 A2C와 다르다.
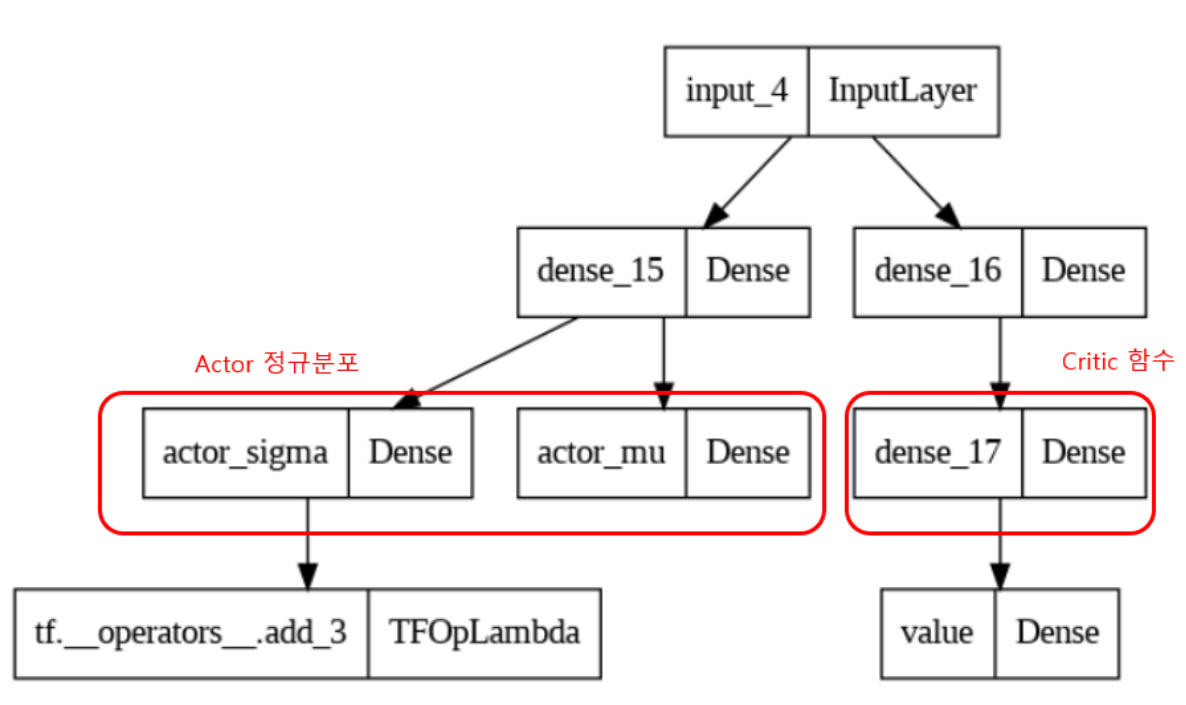
--> 앞에서 A3C의 실습도 진행하였는 데, A3C는 Asynchronous Advantage Actor-Critic의 약어로 아래의 그림에서 처럼 Global Network와 동일한 Local Network를 병렬적으로 생성하고, Local Network의 다양한 환경에서 얻은 데이터를 바탕으로 Global Network의 parameter를 업데이트하는 방향으로 진행한다. 여기서 Action 을 선택할 때 사용되는 신경망인 정책신경망을 Continuos A2C와 동일하게 사용하는 것만 변경하면 Continuos Action을 사용하는 Mountain Car환경에서 사용할 수 있다.

2) 코드 - A3C에서 변경이 필요한 부분
2-1) Action 선택 ( 정규분포에서 선택 )
# 정책신경망의 출력을 받아 확률적으로 행동을 선택
def get_action(self, state):
mu, sigma, _ = self.local_model(state)
dist = tfd.Normal(loc=mu[0], scale=sigma[0])
action = dist.sample([1])[0]
action = np.clip(action, -self.max_action, self.max_action)
return action , dist-> Normal 분포에서 Action을 선택하며, Env에서 사용하는 Action의 상하한을 적용해준다.
2-2) Loss 계산 시 action_prob ( π(a|s) 를 계산할 때 사용함)
# 저장된 샘플들로 A3C의 오류함수를 계산
def compute_loss(self):
discounted_prediction = self.discounted_prediction(self.rewards)
discounted_prediction = np.array(discounted_prediction).reshape(len(discounted_prediction),-1) ### (999,) => (999,1) 로 2차원으로 변경
# discounted_prediction = tf.convert_to_tensor(discounted_prediction[:, None],dtype=tf.float32)
# print(f'discounted_prediction shape : {discounted_prediction.shape}')
### policy_prob 와 action_prob가 필요함 --> states가 여러개 이므로 각각이 여러개가 나옴
### 각각의 분포마다 action
actor_mus, actor_sigmas, values = self.local_model(np.array(self.states))
# print(f'actor_mus : {len(actor_mus)} , actor_sigmas : {len(actor_sigmas)} . values : {len(values)}')
# 가치 신경망 업데이트
advantages = discounted_prediction - values
# print(f'advantages shape : {advantages.shape}')
critic_loss = 0.5 * tf.reduce_sum(tf.square(advantages))
# print(f'critic_loss shape : {critic_loss}')
# 정책 신경망 업데이트 --> action_prob가 필요함
action = tf.convert_to_tensor(self.actions, dtype=tf.float32)
# print(f'action shape : {action.shape}')
## dist = policy (action 확률분포) 각각의 action에 맞는 확률분포를 선택함
for i, item in enumerate(zip(actor_mus, actor_sigmas, action)):
mu = item[0][0]
sigma = item[1][0]
action = item[2][0]
## policy_prob
dist = tfd.Normal(loc=mu, scale=sigma)
# self.policy_prob.append(dist)
## action_prob
action_prob = dist.prob([action])[0]
self.action_prob.append(action_prob)
cross_entropy = - tf.math.log(action_prob + 1e-10)
actor_loss = tf.reduce_sum(cross_entropy * tf.stop_gradient(advantages))
total_loss = 0.5 * critic_loss + actor_loss
# print(f'total_loss : {total_loss}')
return total_loss-> Action prob를 계산을 위해 states 배열에 있는 상태 정보를 신경망에 넣은 뒤 states 수에 맞게 출력되는 mu (평균), sgima (표준편차)로 각각의 정규분포를 만들고 아래와 같이 action_prob를 구하여 배열에 저장한다.
for i, item in enumerate(zip(actor_mus, actor_sigmas, action)):
mu = item[0][0]
sigma = item[1][0]
action = item[2][0]
## policy_prob
dist = tfd.Normal(loc=mu, scale=sigma) #### 각각의 정규분포
# self.policy_prob.append(dist)
## action_prob
action_prob = dist.prob([action])[0] ### action을 뽑을 action_prob를 구함
self.action_prob.append(action_prob)이 값은 cross_entropy를 구하는 데 사용되며 이 값으로 actor 신경망의 loss를 계산한다.
2-3) 정책 / 가치 신경망
# Dnn 모델 생성
def continuos_actor_critic_dnn(self):
### state가 들어감
input_ = keras.layers.Input(shape=(self.state_size))
### Actor (정책평가) -> 정규분포로 변경하기 위해 mu , sigma 생성함 -> 각각의 action에 대한 정규분포를 생성함.
actor_fc = keras.layers.Dense(24, activation='tanh')(input_)
actor_mu = keras.layers.Dense(self.action_size, activation='linear', kernel_initializer=keras.initializers.RandomUniform(-1e-3, 1e-3))(actor_fc)
actor_sigma = keras.layers.Dense(self.action_size, activation='sigmoid', kernel_initializer=keras.initializers.RandomUniform(-1e-3, 1e-3))(actor_fc)
actor_sigma = actor_sigma + 1e-5
## Critic (가치평가)
critic_fc1 = keras.layers.Dense(24, activation='tanh')(input_)
critic_fc2 = keras.layers.Dense(24, activation='tanh')(critic_fc1)
value = keras.layers.Dense(1, kernel_initializer=keras.initializers.RandomUniform(-1e-3, 1e-3))(critic_fc2)
## model
model = keras.models.Model(inputs=[input_], outputs=[actor_mu, actor_sigma, value])
return model-> 신경망은 앞의 Continuos A2C에서 사용한 신경망을 그대로 사용하였다.
** Continuos Mountain Car 문제는 A2C ( A3C ) 로는 해결이 어려우며 연속적인 Action Space를 사용할 수 있는 DDPG 라는 알고리즘이 있는 것으로 알고 있으며 해당 알고리즘을 공부하여 이 문제에 적용해볼 예정이다.
'머신러닝 딥러닝' 카테고리의 다른 글
| [강화학습] DDPG (Deep Deterministic Policy Gradient)실습_ContinuosMountainCar(2/2) (0) | 2023.03.15 |
|---|---|
| [강화학습] DDPG (Deep Deterministic Policy Gradient) 강화학습 (1/2)_이론 (1) | 2023.03.11 |
| [강화학습]A3C_Discrete환경_Cartpole_Mountain_car (2) | 2023.02.24 |
| [강화학습]Continuos A2C(연속적 A2C)_mountain Car (0) | 2023.02.15 |
| [강화학습]A2C (Actor-Critic)CartPole_Mountain Car 문제 (0) | 2023.02.11 |




