| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 사이드프로젝트
- TeachagleMachine
- 클론코딩
- 강화학습
- coding
- 앱개발
- redux
- React
- 데이터분석
- App
- Instagrame clone
- 카트폴
- FirebaseV9
- 조코딩
- 전국국밥
- JavaScript
- clone coding
- 리액트네이티브
- GYM
- pandas
- 머신러닝
- Reinforcement Learning
- python
- Ros
- 강화학습 기초
- kaggle
- ReactNative
- 딥러닝
- expo
- selenium
- Today
- Total
qcoding
[데이터분석실습][이진분류_LR/XGB]Heart Failure Prediction_kaggle 본문
## Kaggle data 분석
https://www.kaggle.com/datasets/andrewmvd/heart-failure-clinical-data
Heart Failure Prediction
12 clinical features por predicting death events.
www.kaggle.com
# 데이터셋 columns
age: 환자의 나이
anaemia: 환자의 빈혈증 여부 (0: 정상, 1: 빈혈)
creatinine_phosphokinase: 크레아틴키나제 검사 결과
diabetes: 당뇨병 여부 (0: 정상, 1: 당뇨)
ejection_fraction: 박출계수 (%)
high_blood_pressure: 고혈압 여부 (0: 정상, 1: 고혈압)
platelets: 혈소판 수 (kiloplatelets/mL)
serum_creatinine: 혈중 크레아틴 레벨 (mg/dL)
serum_sodium: 혈중 나트륨 레벨 (mEq/L)
sex: 성별 (0: 여성, 1: 남성)
smoking: 흡연 여부 (0: 비흡연, 1: 흡연)
time: 관찰 기간 (일)
DEATH_EVENT: 사망 여부 (0: 생존, 1: 사망)
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import matplotlib as mpl
# pd.read_csv()로 csv파일 읽어들이기
df = pd.read_csv('./heart_failure_clinical_records_dataset.csv')
df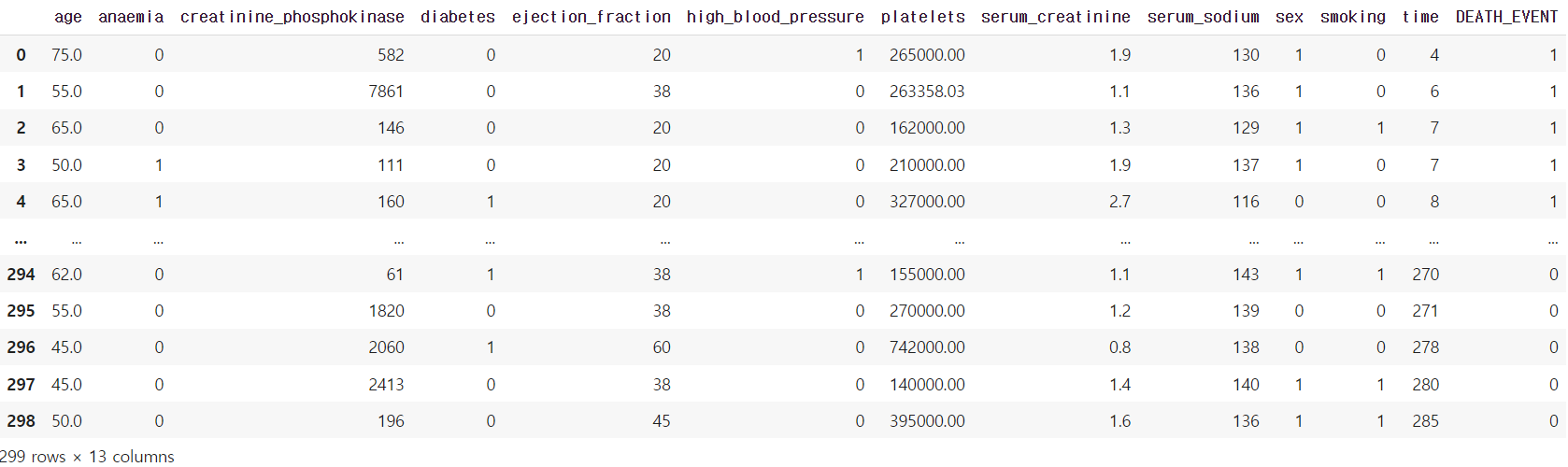
## 데이터 분석하기
# DataFrame에서 제공하는 메소드를 이용하여 컬럼 분석하기 (head(), info(), describe())
df.head()
df.info()
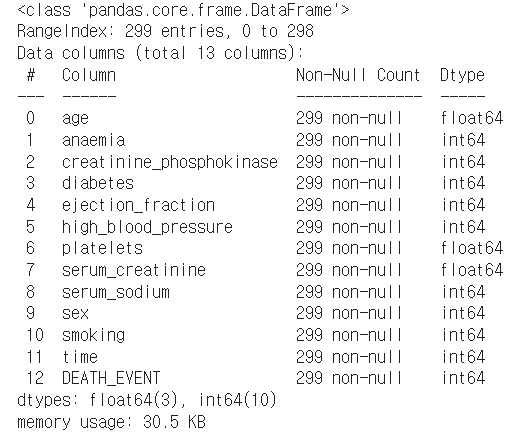
df_g = df.copy()
# seaborn의 histplot, jointplot, pairplot을 이용해 히스토그램 그리기
mpl.rc('font',size=13)
fig , axes = plt.subplots(nrows=5,ncols=2)
# plt.tight_layout()
fig.set_size_inches(11,15)
plt.subplots_adjust(wspace=0.2, hspace=0.8)
axes[0,0]=sns.histplot(x='age' , data=df_g , kde=True ,ax=axes[0,0] , hue='DEATH_EVENT',multiple='dodge')
axes[0,0].set(
title = 'Age'
)
df_g['anaemia']=df_g['anaemia'].astype('str')
axes[0,1]=sns.histplot(x='anaemia' , data=df_g ,ax=axes[0,1],hue='DEATH_EVENT',multiple='dodge')
axes[0,1].set(
title = 'anaemia'
)
df_g['sex']=df_g['sex'].astype('str')
axes[1,0]=sns.histplot(x='sex' , data=df_g ,ax=axes[1,0],hue='DEATH_EVENT',multiple='dodge')
axes[1,0].set(
title = 'sex'
)
axes[1,1]=sns.histplot(x='creatinine_phosphokinase' , data=df_g ,ax=axes[1,1],kde=True)
axes[1,1].set(
title = 'creatinine_phosphokinase'
)
axes[2,0]=sns.histplot(x='ejection_fraction' , data=df_g ,ax=axes[2,0],kde=True)
axes[2,0].set(
title = 'ejection_fraction'
)
axes[2,1]=sns.histplot(x='platelets' , data=df_g ,ax=axes[2,1],kde=True)
axes[2,1].set(
title = 'platelets'
)
axes[3,0]=sns.histplot(x='serum_creatinine' , data=df_g ,ax=axes[3,0],kde=True)
axes[3,0].set(
title = 'serum_creatinine'
)
axes[3,1]=sns.histplot(x='serum_sodium' , data=df_g ,ax=axes[3,1],kde=True)
axes[3,1].set(
title = 'serum_sodium'
)
axes[4,0]=sns.histplot(x='time' , data=df_g ,ax=axes[4,0],kde=True)
axes[4,0].set(
title = 'time'
)
df_g['smoking']=df_g['smoking'].astype('str')
axes[4,1]=sns.histplot(x='smoking' , data=df_g ,ax=axes[4,1],hue='DEATH_EVENT' ,multiple='dodge' )
axes[4,1].set(
title = 'smoking'
)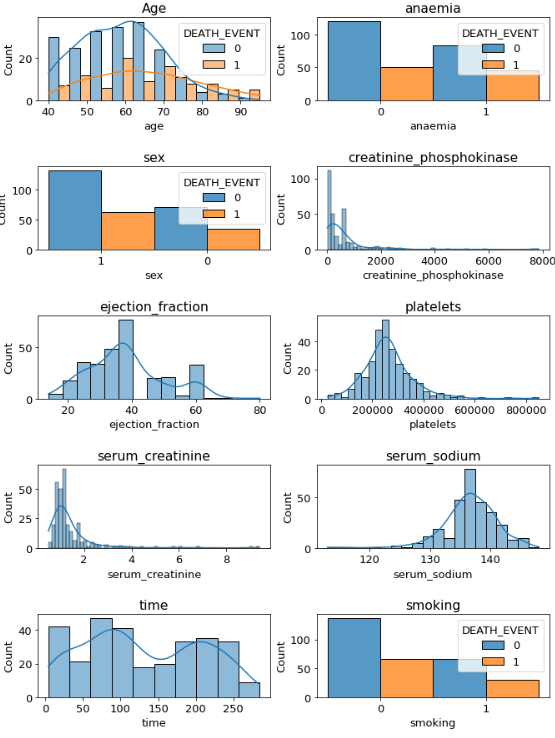
--> 각 피처들을 histplot을 통해 데이터 분포를 확인함.
--> age와 death를 보면 age가 어린쪽에 death가 좀 낮은 경향이 있는 것을 볼 수 있다. anaesia나 sex , smoking의 여부는 death를 가르는 데에 큰 영향을 주는 것 같아 보이진 않는다.
sns.jointplot(x='platelets', y='creatinine_phosphokinase', hue='DEATH_EVENT', data=df, alpha=0.3)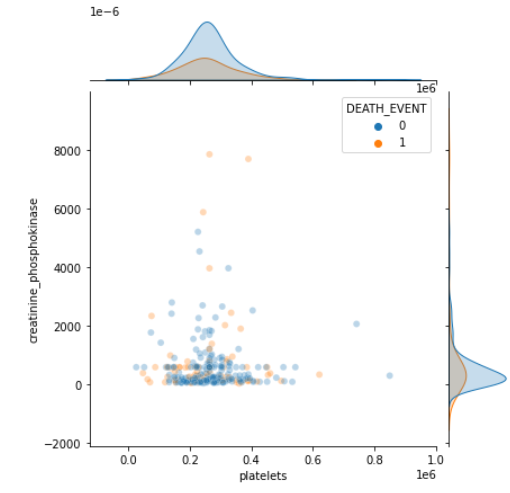
# seaborn의 Boxplot 계열(boxplot(), violinplot(), swarmplot())을 사용
# Hint) hue 키워드를 사용하여 범주 세분화 가능
mpl.rc('font',size=13)
fig , axes = plt.subplots(nrows=3,ncols=2)
# plt.tight_layout()
fig.set_size_inches(11,8)
plt.subplots_adjust(wspace=0.2, hspace=0.8)
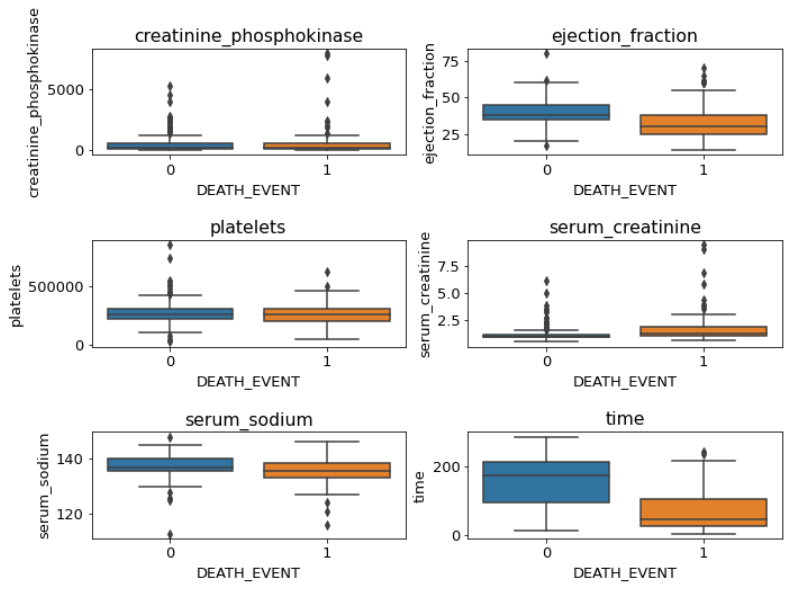
axes[0,0]=sns.boxplot(x='DEATH_EVENT', y='creatinine_phosphokinase' , data=df_g,ax=axes[0,0])
axes[0,0].set(
title = 'creatinine_phosphokinase'
)
axes[0,1]=sns.boxplot(x='DEATH_EVENT', y='ejection_fraction' , data=df_g,ax=axes[0,1])
axes[0,1].set(
title = 'ejection_fraction'
)
axes[1,0]=sns.boxplot(x='DEATH_EVENT', y='platelets' , data=df_g,ax=axes[1,0])
axes[1,0].set(
title = 'platelets'
)
axes[1,1]=sns.boxplot(x='DEATH_EVENT', y='serum_creatinine' , data=df_g,ax=axes[1,1])
axes[1,1].set(
title = 'serum_creatinine'
)
axes[2,0]=sns.boxplot(x='DEATH_EVENT', y='serum_sodium' , data=df_g, ax=axes[2,0])
axes[2,0].set(
title = 'serum_sodium'
)
axes[2,1]=sns.boxplot(x='DEATH_EVENT', y='time' , data=df_g, ax=axes[2,1])
axes[2,1].set(
title = 'time'
)
## scaling
from sklearn.preprocessing import StandardScaler
# 수치형 입력 데이터, 범주형 입력 데이터, 출력 데이터로 구분하기
X_number = df[['age', 'creatinine_phosphokinase','ejection_fraction', 'platelets','serum_creatinine', 'serum_sodium']]
X_category = df[['anaemia', 'diabetes', 'high_blood_pressure', 'sex', 'smoking']]
y = df['DEATH_EVENT']
print(f'수치형데이터 :{X_number.shape} , {X_number.columns}')
print(f'범주형데이터 :{X_category.shape}, {X_category.columns}')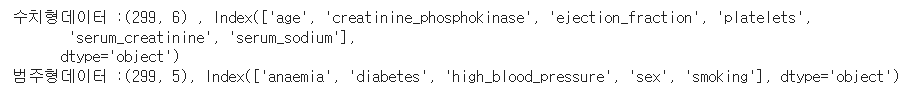
# 수치형 입력 데이터를 전처리하고 입력 데이터 통합하기
scaler =StandardScaler()
X_number_scaled = scaler.fit_transform(X_number)
X_number_scaled_df = pd.DataFrame(X_number_scaled , columns=X_number.columns , index=X_number.index)
X=pd.concat([X_number_scaled_df,X_category] , axis=1)
X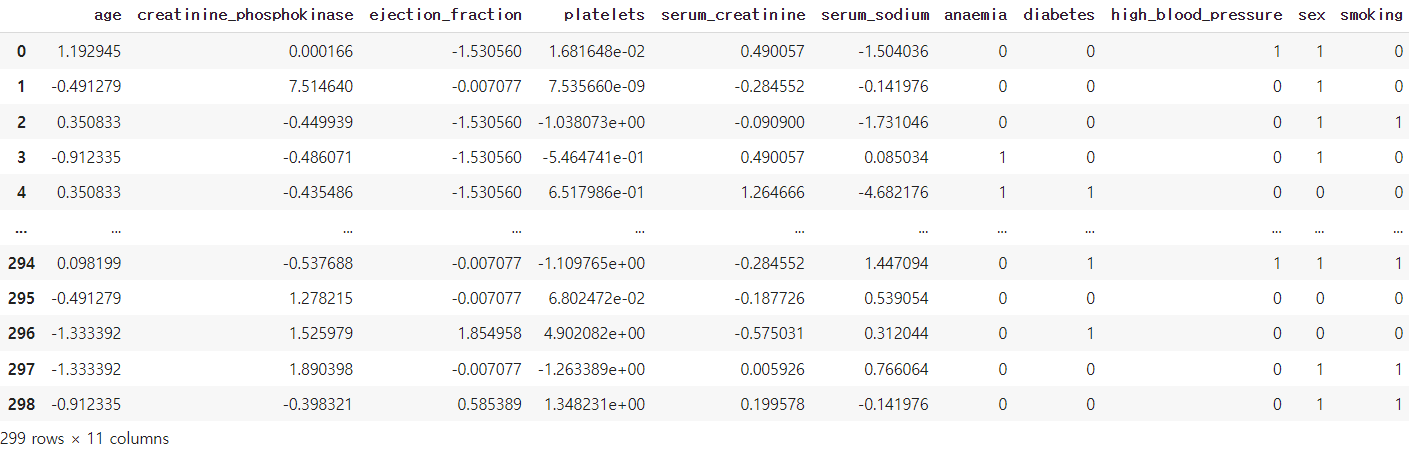
## 모델학습
1) LogisticRegression
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report,confusion_matrix
# LogisticRegression 모델 생성/학습
model_lr = LogisticRegression(max_iter=1000)
model_lr.fit(X_train, y_train)
# Predict를 수행하고 classification_report() 결과 출력하기
pred = model_lr.predict(X_test)
print(classification_report(y_test, pred , target_names=['Survive','Death']))
--> 이 문제에서는 평가지표중에서 Recall이 precision보다 더 중요하다. 그 이유는 Recall은 아래식과 같이 실제 정답인 값 중에서 내가 정답으로 예측한 비율을 말한다. Recall이 중요한 경우는 FN이 높으면 안되는 즉, Negative라고 예측해서 틀린경우이다. 해당 문제는 각 종 지표를 가지고 환자의 죽음을 예측하는 것으로 잘못된 예측의 경우 보는 피해가 상당하다. 예를 들어서 문제가 있는 환자를 Survive로 잘 못예측했을 때 그 잘못으로 환자가 수술이나 치료를 받지 못할 경우에 목숨이 위태로울 수 있는 문제가 있으므로 Recall이 중요하다고 할 수 있다.
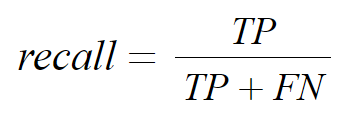
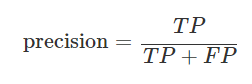
--> 위의 Classfication_report를 통해서 확인하면, preicison Death는 1.00 이고 recall Death는 0.38이다. 이를 해석하면
Death라고 예측한 것 중에서는 precision = 3 / (3+0) = 1.0 , recall = 3 /( 3+5) = 0.38 로 positive라고 예측한 것 중에서는 Death를 다 맞게 예측하였으나, 실제 Death 가 될 사람들 중에서는 38%정도밖에 예측하지 못한 결과이다. negative라고 예측했는데 틀린 FN이 5명이나 되기 때문에 해당 모델의 성능은 안좋다고 볼 수 있다.
2) XGBClassifier
from xgboost import XGBClassifier
# XGBClassifier 모델 생성/학습
model_xgb = XGBClassifier()
model_xgb.fit(X_train,y_train)
# Predict를 수행하고 classification_report() 결과 출력하기
pred = model_xgb.predict(X_test)
print(classification_report(y_test, pred , target_names=['Survive','Death']))
print(confusion_matrix(y_test,pred))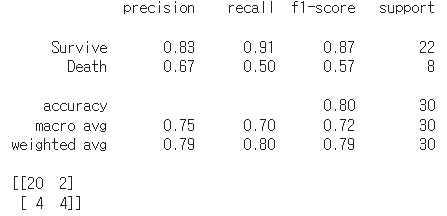
-> xbgClassifier 의 경우는 30명을 예측했을 때 기준으로 precision은 떨어졌고 recall은 0.5로 올라간 것을 볼 수 있다. 1명밖에 차이가 안나지만 FN의 경우 5->4로 줄었으며, TP 3->4로 1명이 늘었음을 알 수있다.
# XGBClassifier 모델의 feature_importances_를 이용하여 중요도 plot
importance = model_xgb.feature_importances_
importance_df = pd.DataFrame(importance ,index=X.columns ,columns=['feature_importance']).sort_values('feature_importance', ascending=False)
importance_df
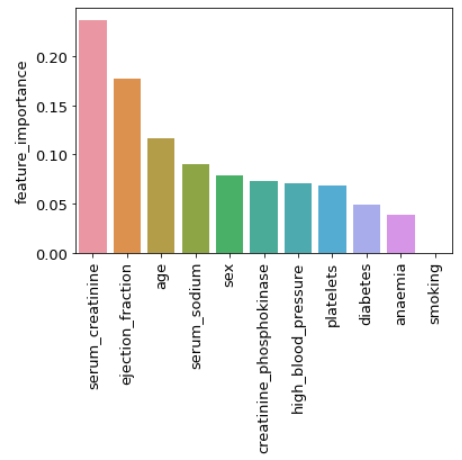
ax=sns.barplot(x=importance_df.index, y='feature_importance',data=importance_df)
ax.tick_params(axis='x',labelrotation = 90)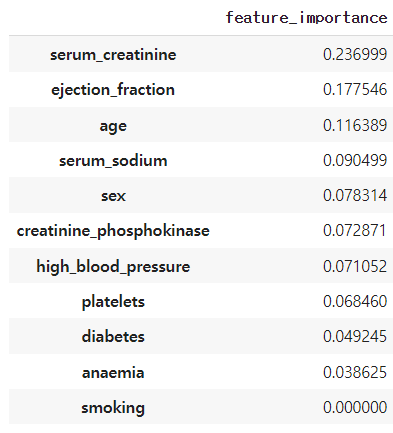
## precison / recal curve
from sklearn.metrics import plot_precision_recall_curve
fig , ax =plt.subplots()
fig.set_size_inches(11,6)
plot_precision_recall_curve(model_lr,X_test,y_test , ax=ax)
plot_precision_recall_curve(model_xgb,X_test,y_test, ax=ax)
ax.set(
title = 'Precison Recall Curve'
)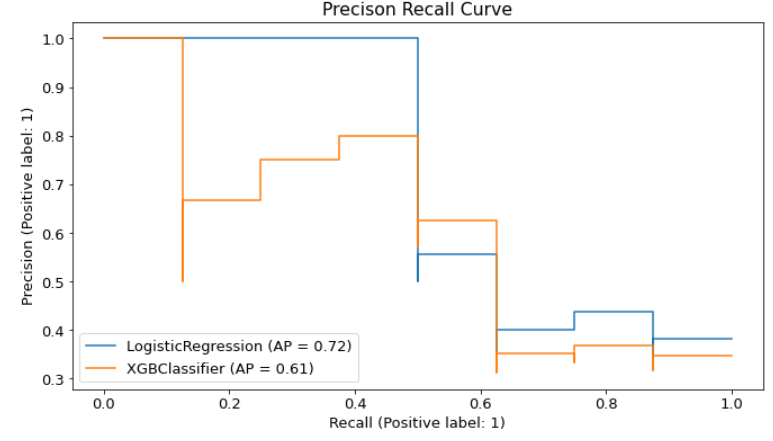
--> Recall과 Precision을 수치별로 그릴 수 있는 것으로, Recall을 유지하면서 어느정도의 precision을 낼 수 있는 지를 확인해 볼 수 있다. Recall을 올리기 위해선 FN, 즉 Negative라고 말해서 False가 되는 경우를 줄여야 되는 데, 이는 즉 Negative라고 예측을 하지 않게 되고 positive라고 예측을 많이 하게 되는 것이며, positive라고 예측을 할 경우 당연히 틀리는 확률이 높아지면 FP , 즉 Postive라고 예측을 해서 False가 되는 것이 높아지므로 presicion을 떨어지게 된다.
##plot_roc_curve
# 두 모델의 ROC 커브를 한번에 그리기 (힌트: fig.gca()로 ax를 반환받아 사용)
from sklearn.metrics import plot_roc_curve
fig , ax =plt.subplots()
fig.set_size_inches(11,6)
plot_roc_curve(model_lr,X_test,y_test , ax=ax)
plot_roc_curve(model_xgb,X_test,y_test, ax=ax)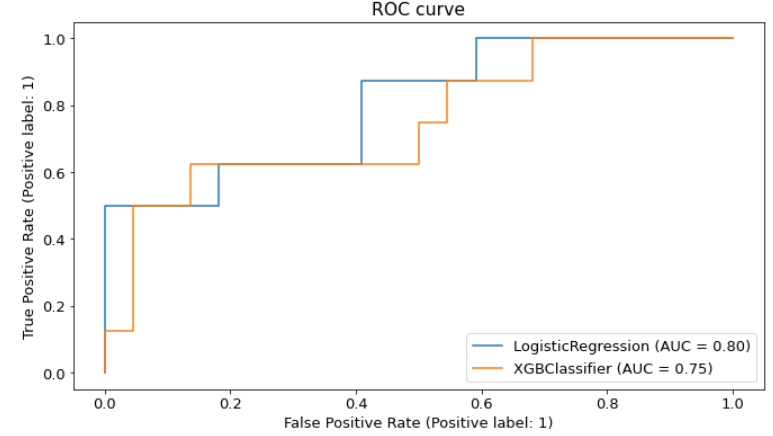
-> Roc Curve는 x축(False Positive Rate)에 비해서 y축(True Positive Rate)의 값이 빠르게 증가하는 경우 면적이 1에 가깝게 채워지게 되는 경우 성능이 좋은 모델로, 두 모델의 성능차이는 크게 없는 것으로 확인할 수 있다.
'Python 데이터분석' 카테고리의 다른 글
| [데이터 분석 시 유용한 기능 정리] - 필요부분 검색 (1) | 2023.12.06 |
|---|---|
| [데이터분석실습][다중분류_LR/XGB]공부 잘하는 것과 연관 된 연구 (0) | 2022.09.01 |
| [데이터분석실습][데이터전처리]스타벅스 고객 데이터 분석하기 (0) | 2022.08.06 |
| [데이터분석 실습][데이터전처리]구글플레이스토어 데이터 분석 (1) | 2022.07.29 |
| [데이터 분석실습]타이타닉 데이터 (0) | 2022.07.23 |




