| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- kaggle
- React
- coding
- 딥러닝
- FirebaseV9
- Reinforcement Learning
- clone coding
- 데이터분석
- Ros
- 사이드프로젝트
- Instagrame clone
- 전국국밥
- pandas
- 카트폴
- ReactNative
- App
- GYM
- 앱개발
- selenium
- JavaScript
- python
- TeachagleMachine
- 클론코딩
- 조코딩
- expo
- 리액트네이티브
- 강화학습 기초
- redux
- 강화학습
- 머신러닝
- Today
- Total
qcoding
[SARIMA]빌딩 전력 시계열 모델 예측 본문
* Bulding 소모 전력 예측을 위한 시계열 모델인 SARIMA 모델 사용방법
=> 제공된 데이터는 2018-07-01 00:00:00 ~ 2019-12-31 23:59:00 까지의 데이터로 1분단위의 전기제품의 kw 의 소모량으로 되어 있는 데이터 set임
=> 분단위 데이터는 너무 많으므로 최종적으로 일단위로 묶어서 일별 소모 전력량을 예측하는 모델을 만들어 봄.
1) 데이터 주중 / 주말 패턴 분리
2) 최소 단위의 계절성 성분 찾기
3) 예측할 데이터 프레임 생성
4) pmd arima 사용
5) 예측하기
5-1) n_period를 test 사이즈와 동일하게 한번에 예측하기
5-2) n_period를 1개씩 추가하여, 새로운 관측치가 들어올때 마다 모델을 학습한 후 예측수행
1) 데이터 주중 / 주말 패턴 분리
### 라이브러리 import
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.stattools import acf,pacf
import statsmodels.api as sm
import statsmodels.tsa.api as smt
from sklearn.metrics import r2_score, mean_squared_error
from statsmodels.tsa.statespace.sarimax import SARIMAX
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import pmdarima as pm### plot 함수
def test_stationarity(ts):
MA = ts.rolling(window=96).mean() ### window 안에는 몇개의 데이터를 사용할 것 인지 정의
MSTD = ts.rolling(window=96).std()
#plot
plt.figure(figsize=(15,5))
origin = plt.plot(ts, color='blue', label='origin')
mean = plt.plot(MA, color='red', label='Rolling Mean')
std = plt.plot(MSTD, color='green', label='Rolling Std')
plt.legend(loc='best')
plt.title('Rolling Mean & Std')
plt.show(block=False)
def tsplot(y, lags=None, figsize=(10,5), style='bmh', maxlag=300 ):
if not isinstance(y,pd.Series):
y=pd.Series(y)
with plt.style.context(style):
fig = plt.figure(figsize=figsize)
layout=(2,2)
ts_ax = plt.subplot2grid(layout, (0,0), colspan=2)
acf_ax = plt.subplot2grid(layout, (1,0))
pacf_ax = plt.subplot2grid(layout, (1,1))
y.plot(ax=ts_ax)
result = sm.tsa.stattools.adfuller(y, autolag='AIC', maxlag=maxlag)
ts_ax.set_title(f"PLOT Dickey-Fuller : p-value:{result[1] : .3f} ")
smt.graphics.plot_acf(y, lags=lags, ax=acf_ax)
smt.graphics.plot_acf(y, lags=lags, ax=pacf_ax)
plt.tight_layout()
print(f'ADF Statistic : {result[0] :.3f}')
print(f'n_lags : {result[2]}')
print(f'p-value : {result[1]}')
for key,value in result[4].items():
print('Critical Values')
print(f' {key} , {value}')### 데이터 로드
# ▶ pd.set option
import pandas as pd
pd.set_option('display.max_columns',100)
pd.set_option('display.max_rows',100)
file_path = './drive/MyDrive/Project/arima/arima_model.gz'
df = pd.read_pickle(file_path)
df.head()
데이터 형태는 192개의 열이 있으며, 이중 (kw)로 표기된 것은 전기제품의 전력 소비량을 의미한다.
# Colums 내에 'KW'들어 있는 항을 가지고 합산
df_powerMeter = df.loc[:, df.columns.str.contains('kW')].copy()
# Sum up demands of all power meters
df_powerMeter = df_powerMeter.sum(axis=1).rename('load')
df = pd.DataFrame(df_powerMeter)전체 부하를 계산하기 위해 columns의 이름에서 'kw'를 포함된 열들을 모아서 axis=1 (열)방향으로 다 더하고 'load' columns을 추가한다.

## Feature 생성
### feature 생성
df = df.reset_index()
df['year']=df['Date'].dt.year
df['month']=df['Date'].dt.year
df['hour']=df['Date'].dt.hour
df['weekday']=df['Date'].dt.weekday
df['day'] = df['Date'].dt.day
df['date']=df['Date'].dt.strftime('%Y-%m')
df['year_day']=df['Date'].dt.date
df['workingday'] = np.where(df['weekday']>4, 0, 1)
df
### 주말과 주중 데이터 분리 => 전기요금의 사용패턴이 주말과 주중이 다른 것은 plot 또는 group 하여 평균을 비교해서 알수 있음
# ▶ 주중, 주말 비교
df.groupby('workingday')['load'].mean()
# ▶ 요일 비교
sns.distplot(df[df['weekday']==0]['load'], label='Mon');
sns.distplot(df[df['weekday']==1]['load'], label='Tue');
sns.distplot(df[df['weekday']==2]['load'], label='Wed');
sns.distplot(df[df['weekday']==3]['load'], label='Thr');
sns.distplot(df[df['weekday']==4]['load'], label='Fri');
sns.distplot(df[df['weekday']==5]['load'], label='Sat');
sns.distplot(df[df['weekday']==6]['load'], label='Sun');
plt.legend()
plt.xlim(0,1000)
plt.gcf().set_size_inches(8, 5)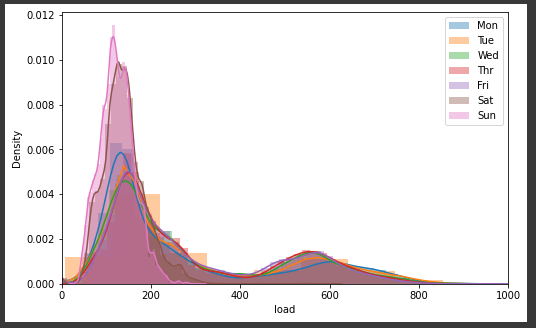
# ▶ 평일 주말 비교
sns.distplot(df[df['workingday']==0]['load'], label='weekend');
sns.distplot(df[df['workingday']==1]['load'], label='weekday');
plt.legend()
plt.xlim(0,1000)
plt.gcf().set_size_inches(8, 5)
displot을 통해 분포를 보면 주말과 주중의 분포가 다른 것을 확인할 수 있다.
2) 최소 단위의 계절성 성분 찾기
-> ARIMA 모델은 Trend(추세)를 반영하여 예측하지만, Seasonal(계절성) 성분을 반영하지 못하므로 SARIMAX를 사용하는데, 이때 SARIMAX의 최소기준이 되는 계절성 성분을 찾기 위해 추론통계를 사용함.
-> 데이터가 1분 단위로 너무 많으므로 DAY (일) 기준으로 그륩하여 예측에 사용함.
group_date = df.groupby(['date'], as_index=False).agg(
avg_load = ('load', 'mean')
)
group_date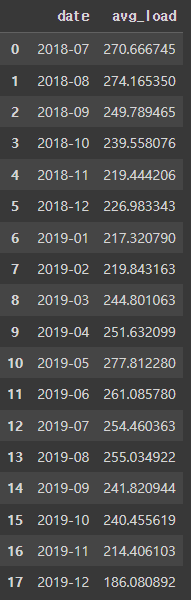
fig, ax = plt.subplots()
fig.set_size_inches(15,5)
sns.lineplot(x='date', y='avg_load', data=group_date, ax=ax)
ax.tick_params(axis='x', labelrotation=45)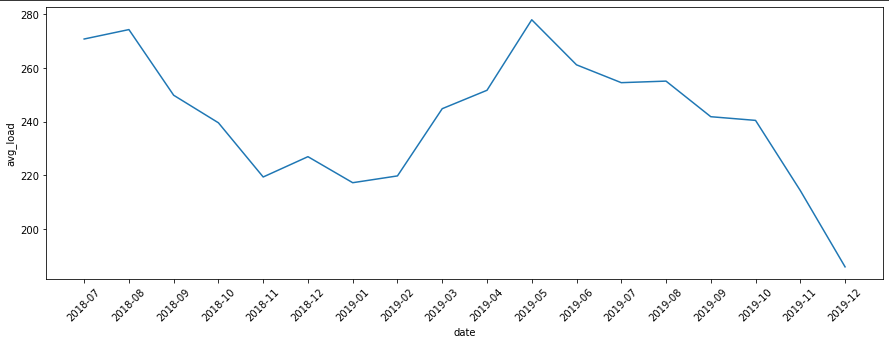
우선 월별로 묶어서 데이터의 경향을 파악함. 그래프를 통해 보면 대략 2018-07 ~ 2019-02까지 패턴과 2019-05~ 2019-8의 패턴이 비슷하게 느껴 지는 데 실제로 추론통계를 통해 확인함
tsplot(group_date['avg_load'], maxlag=7)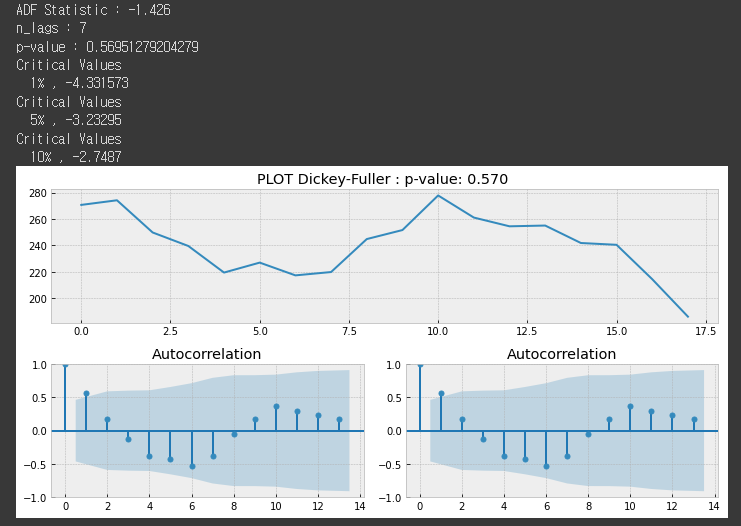
p-value가 0.57로 0.05보다 크므로 비정상성 (일정한 패턴이 있음)을 의미함. 여기서 lag는 maxlag까지 계절성이 있는 것을 찾는 데, 너무 작으면 계절성이 나오기 전에 lag를 그만수행하여 결과가 이상할 수 있음. maxlag를 최대한 크게 잡아서 계절성 패턴이 있을지도 모르는 범위를 놓치면 안됨.
위에서 lag = 7 일때의 데이터를 plot해보면 아래와 같은 범위에서 계절성 패턴을 찾았음을 알수 있다.
아마 3-> 5와 5->7의 패턴이 계절성이 있음을 말해주는 것 같다.
group_date.iloc[:8].plot()
### 예측은 일단위로 데이터를 묶어서 일단위로 수행해야 함으로 group으로 다시 묶어준다.
group = df.groupby(['year_day'], as_index=False).agg(
avg_load = ('load', 'mean')
)
group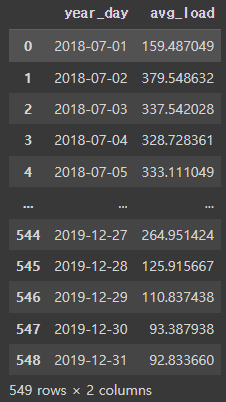
fig, ax = plt.subplots()
fig.set_size_inches(15,5)
sns.lineplot(x='year_day', y='avg_load', data=group, ax=ax)
ax.tick_params(axis='x', labelrotation=45)
위에서 plot해보면 눈으로 봐도 일단위의 계절성이 가장작은 주기를 가지며, 반복되는 것을 확인할 수 있다.
### 성분분해
### 성분분해
dec = sm.tsa.seasonal_decompose(group['avg_load'], period=31, model='addictive').plot() ###
dec.set_size_inches(8,8)
성분 분해를 해보면, Trend / Seasonal / Residual 로 나눠지며, Trend는 ARIMA로 Seasonal은 (P,D,Q,M)을 사용하는 SARIMAX에서 고려될 수 있다. Seasonal이 존재하는 것을 분명히 확인할 수 있다.
눈으로 확인가능하지만, 추론통계를 통해서 다시 한번 확인하도록 한다.
tsplot(group['avg_load'], maxlag=6)
눈으로는 계절성을 확인했는데, 위에서 보면 p-value가 0.001로 0.05보다 작으므로 데이터를 정상성으로 파악한 것을 볼 수 있다. 이것이 처음에 매우 이상했는데, 다시 보면 maxlag가 너무 낮아서 그런 것이다. maxlag가 너무 낮아서 데이터의 계절성을 반영하지 못할 만큼 작은 범위만 보았을 때 다음과 같이 나타난다. 7번째까지의 데이터를 그려 보면 아래와 같다.
group.iloc[:6]['avg_load'].plot()
위의 그림을 보면 maxlag=7일때는 아무런 계절성을 찾을 수 없는 것을 볼 수 있다. 그러므로 maxlag를 늘려서 계절성패턴이 나올 수 있는 범위까지 확인을 해야한다.
tsplot(group['avg_load'], maxlag=20)
group.iloc[:21]['avg_load'].plot()
위에서 maxlag=20으로 늘리면 위와 같이 계절성패턴을 찾은 것을 볼 수 있다.
=> max lag를 어떻게 잡아야 하는지 좀 헷갈리는데, 대략적으로 이해한것을 정리하면 다음과 같다.
전체의 데이터 길이에서 계절성 성분이 존재하려 한다면, 최소한 한번은 동일한 패턴이 나와야 이것이 반복되고 있으므로 계절성을 가지고 있다고 판단할 수 있다. 예를 들어 총 10개 길이의 데이터 인데, 2개로 나누어 보면 5개의 데이터가 패턴을 찾을 수 있는 max_lag 라고 생각하면 이해하기 쉽다. ( 라이브러리에서는 이보다 작은 3정도를 허용하도록 하는 것 같다.)
정리하면 maxlag는 최대탐색할 lag를 의미하며, 그 안에 있는 모든 lag를 계산하여 AIC기준으로 작게만드는 lag를 찾게 되는데 0번째 데이터가 최대 (0 + maxlag)th 번째안에 계절성 패턴이 있는 지를 탐색하는 것을 말한다.
이렇게 1번째 -> (1+maxlag)th 이내 , 2번쨰 -> (2+maxlag)th 이내.... 로 탐색하게 된다. 이때 maxlag는 위에서 말한 것처럼 전체 length/2 보다 작아야 하는데, 그 이유는 n번째 + maxlag 했을 때 전체 데이터의 갯수가 넘어버리면 안되기 떄문이다.
=> 여기서 하루 day(일) 주기로는 계절성이 일어나는데, 만약 그것보다 더 작은 단위로 계절성이 있는 지 확인하기 위해서 즉 시간단위에서 반복이 되는 계절성 성분이 있는 것을 확인하기 위하여, 모든 일자의 시간별 전력량 패턴을 확인해 보자.
### pivot table을 만들어 하루동안의 시간변화 확인
day_idx = df['hour']
day_colums = df['year_day']
day_pivot = df.pivot_table(index=day_idx, columns=day_colums, values='load', aggfunc='mean', fill_value=0)
day_pivot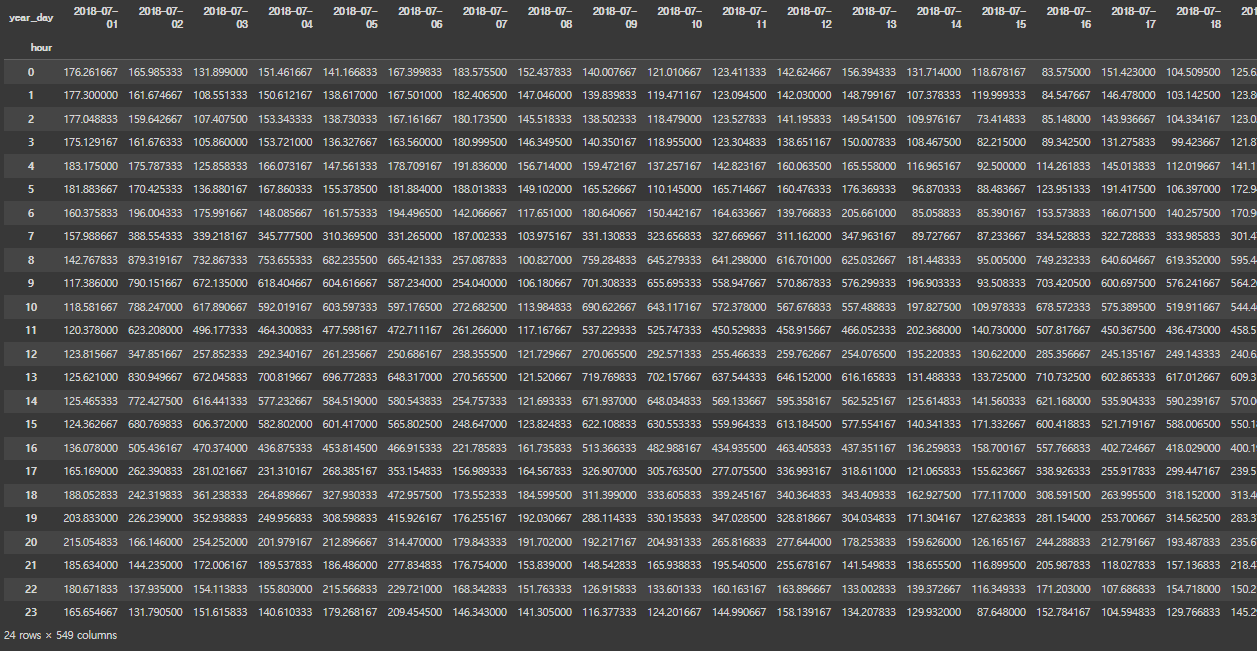
## 시간대별 plot으로 확인
# UB, LB 계산을 위해 평균 및 표준편차 구하기
day_pivot['mean'] = day_pivot.apply(np.mean, axis=1)
day_pivot['std'] = day_pivot.apply(np.std, axis=1)
day_pivot[['mean', 'std']].head(5)
#df_temp_pivot.head()
# UB, LB
day_pivot['UB'] = day_pivot['mean'] + 2*day_pivot['std']
day_pivot['LB'] = day_pivot['mean'] - 2*day_pivot['std']
plt.figure(figsize=(24,12));
day_pivot.plot(figsize=(15,5),color='blue',alpha=0.1,legend=False);
plt.plot(day_pivot.index, day_pivot['UB'], linestyle='--', color='red');
plt.plot(day_pivot.index, day_pivot['LB'] , linestyle='--', color='red');
plt.xticks(range(0,25));
plt.legend(['demand', 'Upper Bound', 'Lower Bound']);
위의 그림에서 살펴보면, 시간단위에도 계절성 성분이 존재하는 것을 볼수 있다. 6~12시 까지와 12시에서 18시까지의 패턴이 반복되고 있으며 여기서 볼때 최소단위의 패턴은 일(day)가 아닌 시간(time)까지 분해해주어야 분(minute)단위의 예측이 가능함을 알 수 있다. 추론통계량을 보면 아래와 같다.
## 임의의 일자 sample
tsplot(day_pivot.iloc[:,1], maxlag=10)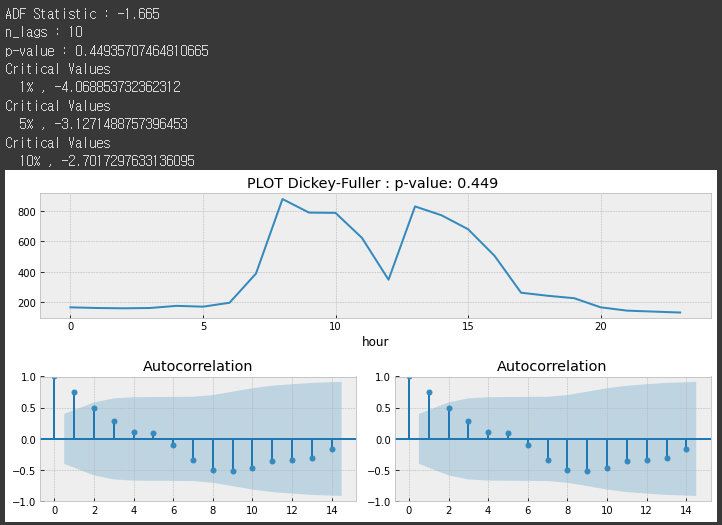
### 성분분해
dec = sm.tsa.seasonal_decompose(day_pivot.iloc[:,1], period=4, model='addictive').plot() ###
dec.set_size_inches(8,8)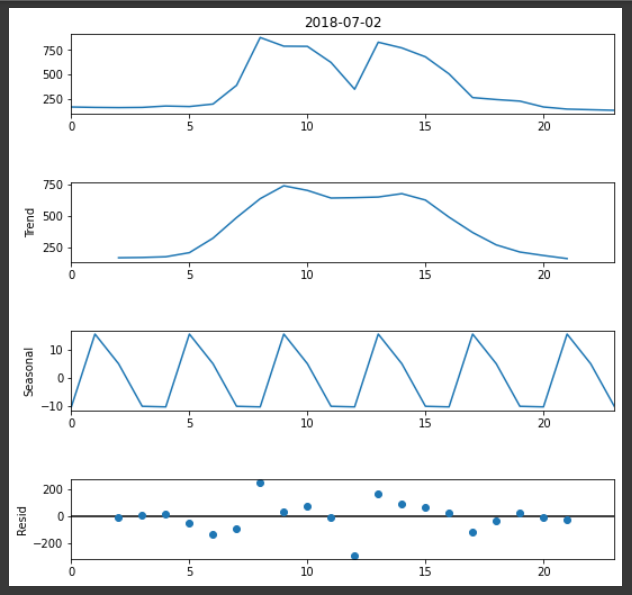
=> 성분분해결과 Trend(추세)와 Sesonality(계절성) 존재하는 것으로 보이며, 이것은 분단위 예측을 수행할 때 분단위 데이터내에 있는 계절성을 예측할 수 있는 SARIMAX 모델이 필요하다는 것을 의미한다.
=> 여기서는 일단위 예측으로 사용하려고한다. pmd auto arima를 사용하려고 할 때 데이터가 너무 많으면 메모리 문제가 발생한다.
3) 예측할 데이터 프레임 생성
df_fil = df.groupby(['year_day'], as_index=False).agg(
avg_load = ('load', 'mean')
)
df_fil['year_day'] = pd.to_datetime(df_fil['year_day'])
df_fil = df_fil.set_index('year_day')
df_fil
### 전체 데이터에서 train / test 부분 나눔
# df = df.set_index('Date')
criteria = '2019-05-31'
y_train = df_fil.loc[df_fil.index <= criteria]
y_test = df_fil.loc[df_fil.index > criteria]
y_train.shape , y_test.shape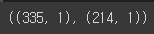
4) pmd arima 사용
### seaonal 성분은 일단위 패턴이 있으므로 1분단위 데이터 * 60 (=1시간) * 24 = 1440 개
### 일단위 데이터면
auto_arima_model = pm.auto_arima(
y_train['avg_load'],
start_p=0,d=1,start_q=0,
max_p=3,max_d=1,max_q=3,
start_P=0, D=1, start_Q=0,
max_P=3,max_D=1,max_Q=3,
m=7,
trace=True,
error_action='ignore',
suppress_warnings=True,
stepwise=False
)
auto_arima_model.summary()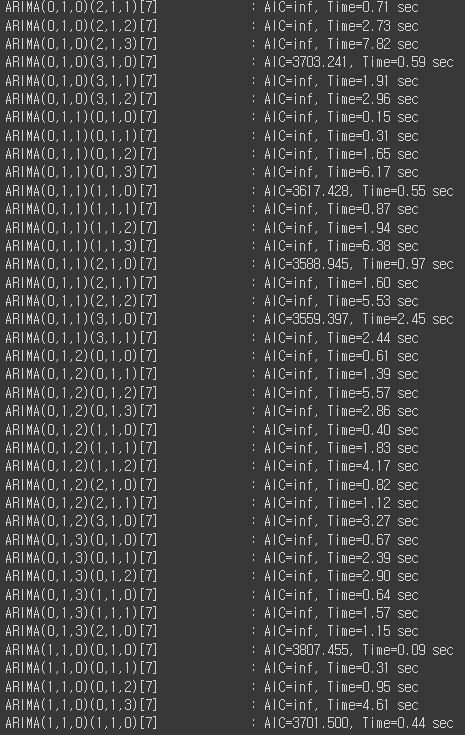

자동으로 계산되며 ARIMA(0,1,1)(3,1,0)[7] 모델이 best 모델로 결정된 것 을 알 수 있다.
여기서 m 은 seasonal 주기를 의미하며, 일단위 데이터로 하기 때문에 주(7일)을 반영하여 7로 설정하였다.
5) 예측하기
5-1) n_period를 test 사이즈와 동일하게 한번에 예측하기
=> 예측할 때 y_test와 같은 수의 여기서는 241개를 한번에 예측하는 코드이다. 아무래도 한번에 여러 step을 예측하므로 정확도가 좀 떨어 질 수있다.
pred = auto_arima_model.predict(n_periods =len(y_test), return_conf_int=True)
pred_val = pred[0]
# pred_ub = pred[1][:,0]
# pred_lb = pred[1][:,1]
pred_index = list(y_test.index)
r2 = r2_score(y_test['avg_load'].values, pred_val)
fig, ax = plt.subplots(figsize=(12, 6))
df_fil['avg_load'].plot(ax =ax)
ax.vlines(criteria,0, 400, linestyle='--',color='r', label='Start of Forecast')
ax.plot(pred_index, pred_val, label='Prediction')
# ax.fill_between(pred_index, pred_lb, pred_ub, color='k', alpha=0.1, label='0.95 pred Interval')
ax.legend(loc='upper left')
rmse = np.sqrt(mean_squared_error(y_test['avg_load'].values, pred_val))
print('Test RMSE: %.3f' % rmse)
plt.suptitle(f' Pred Result R^2 score : {round(r2, 2)} / RMSE : {rmse : .3f}')
plt.show()

5-2) n_period를 1개씩 추가하여, 새로운 관측치가 들어올때 마다 모델을 학습한 후 예측수행
=> 이 방법은 n_period를 1개 예측하고, y_test에서 새로운 관측치 한개를 다시 history (학습) 데이터 넣고 모델을 다시학습한뒤 다시 1개를 예측하는 것을 반복해서 하므로, 시간이 오래 걸리지만 예측은 좀더 정확할 수 있다. 그 이유는 y_test (관측치)가 계속계속 반영되므로 ARIMA의 p,d,q PDQ 들의 feature의 수가 이미 정해져 있다고 해도 parameter의 weights를 새로운 관측치에 맞게 업데이트 할수 있기 때문이다.
# Best model: ARIMA(0,1,1)(3,1,0)[7]
history = [x for x in y_train['avg_load']]
predictions = list()
# walk-forward validation
for idx in range(len(y_test)):
### 위에서 생성한 모델 생성
model = SARIMAX(history, order=(0,1,1), seasonal_order = (3,1,0,7),initialization='approximate_diffuse')
## 학습하기
model_fit = model.fit()
## n개를 예측하기
output = model_fit.forecast(n_periods=1)
## 측할 결과를 predcition 배열에 저장
yhat = output[0]
predictions.append(yhat)
## y_test의 값은 새로운 값이므로, 이것을 다시 history에 넣어음
obs = y_test.iloc[idx]['avg_load']
history.append(obs)
print('predicted=%f, expected=%f' % (yhat, obs))
# evaluate forecasts
rmse = np.sqrt(mean_squared_error(y_test, predictions))
print('Test RMSE: %.3f' % rmse)
### prediction 데이터를 test index와 동일하게 변환
predictions_df=pd.DataFrame(predictions , index=y_test.index)
# plot forecasts against actual outcomes
plt.figure(figsize=(15,5))
plt.plot(y_train,label="Training")
plt.plot(y_test,label="Test")
plt.plot(predictions_df,label="Predicted")
plt.legend(loc = 'best')
plt.tick_params(axis='x',labelrotation=45)
plt.show()


결과를 보면 첫번째가 RMSE : 72.6 이고 두번째가 52.3으로 차이가 꽤 나는 것을 볼 수 있다.
'시계열분석_python' 카테고리의 다른 글
| [전력데이터 클러스터링]전력데이터 시간별 클러스터링_GMM (0) | 2023.04.21 |
|---|---|
| [SARIMAX]전력데이터 분석 ( ARIMA + Fourier 계절성 ) (0) | 2023.04.02 |
| [LSTNET]빌딩 전력 수요예측 (Functional 방법) (0) | 2023.03.26 |
| [LSTNET] 빌딩전력예측 딥러닝 (0) | 2023.03.26 |
| [서평이벤트 당첨_이지스퍼블리싱] 점프투 파이썬_라이브러리 예제편 (0) | 2022.05.27 |




