| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- expo
- 딥러닝
- selenium
- 카트폴
- 강화학습 기초
- 앱개발
- FirebaseV9
- App
- coding
- 사이드프로젝트
- 머신러닝
- 전국국밥
- redux
- React
- 리액트네이티브
- 강화학습
- JavaScript
- 조코딩
- 클론코딩
- TeachagleMachine
- Ros
- Instagrame clone
- clone coding
- kaggle
- 데이터분석
- pandas
- GYM
- ReactNative
- python
- Reinforcement Learning
- Today
- Total
qcoding
[전력데이터 클러스터링]전력데이터 시간별 클러스터링_GMM 본문
* 본 실습에서는 시간대별 일정한 패턴을 보이는 전력 데이터를 몇 개의 클러스터로 분류하는 실습이다.
GMM(Gaussian Mixture Model)은 이 모델은 데이터 집합이 여러 개의 가우시안 분포로부터 생성된다고 가정하는 확률적 생성 모델로 데이터의 분포를 여러 개의 가우시안 분포를 합쳐서 모델링하는 것으로 GMM은 분포가 복잡하거나 다중 모드를 가지는 데이터를 모델링하는 데 특히 유용하다. 예를 들어, 이미지나 음성 등 복잡한 데이터를 분석하고 처리하는 데 많이 사용된다.
GMM은 EM (Expectation-Maximization) 알고리즘을 사용하여 모델링되며, 일반적으로 최적의 모델링 결과를 얻기 위해 여러 번의 EM 반복이 필요하다.
정리하면, GMM 모델을 사용하면 데이터가 어디에서 왔는지, 어떤 분포에서 생성되었는지를 확률적으로 추정할 수 있으며, 생성형 모델로 아래와 같은 과정으로 사용된다.
1) 초기값 설정
GMM 학습을 위해 초기값을 설정해야 합니다. 초기값은 가우시안 분포의 개수, 위치, 크기 등을 나타내는 파라미터들입니다. 일반적으로 랜덤으로 초기값을 설정합니다.
2) Expectation-Maximization (EM) 알고리즘
EM 알고리즘은 GMM을 학습하는 데 사용됩니다. 이 알고리즘은 두 단계로 이루어져 있습니다.
3) Expectation step (E-step) : 현재 파라미터를 사용하여 데이터 포인트가 어느 가우시안 분포에 속하는지 확률적으로 추정합니다. 이 때, 추정된 확률 값은 가중치(weight)로 사용됩니다.
Maximization step (M-step) : E-step에서 구한 가중치를 사용하여 새로운 파라미터를 추정합니다. 이 과정에서는 각각의 가우시안 분포의 평균, 공분산 행렬, 가중치 등을 업데이트합니다.
EM 알고리즘은 E-step과 M-step을 번갈아가면서 반복합니다. 이 때, 학습이 수렴할 때까지 반복합니다.
4) 모델 선택
GMM을 학습한 후, 모델 선택을 수행합니다. 모델 선택은 가우시안 분포의 개수를 결정하는 것입니다. 일반적으로 BIC (Bayesian Information Criterion)이나 AIC (Akaike Information Criterion)와 같은 모델 선택 기준을 사용하여 최적의 가우시안 분포 개수를 결정합니다.
5) 예측
GMM을 학습하고 모델을 선택한 후, 새로운 데이터를 분류하거나, 새로운 데이터를 생성하는 등의 예측 작업을 수행할 수 있습니다.
## 실습
### GMM - 시간대별 퍙균값 CLUSTER 에 따른 분류 방법
# DATA 불러오기
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.mixture import GaussianMixture
df = pd.read_csv('./sarimax.csv')
df = df.drop(columns=['Unnamed: 0'], axis=1)
df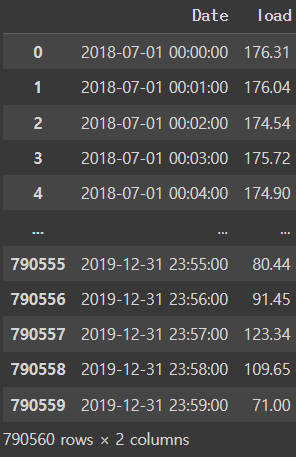
사용한 데이터는 2018/07/01 ~ 2019/12/31일 까지 1분 단위의 전력데이터이다.
# 일자별 시간별 데이터 정리
def creating_feature(df):
### feature 생성
df['Date'] = pd.to_datetime(df['Date'])
df['year']=df['Date'].dt.year
df['month']=df['Date'].dt.year
df['hour']=df['Date'].dt.hour
df['weekday']=df['Date'].dt.weekday
df['day'] = df['Date'].dt.day
df['date']=df['Date'].dt.strftime('%Y-%m')
df['year_day']=df['Date'].dt.date
df['workingday'] = np.where(df['weekday']>4, 0, 1)
return df
## pivot table
def create_pivot_table(df):
day_idx = df['hour']
day_colums = df['year_day']
day_pivot = df.pivot_table(index=day_idx, columns=day_colums, values='load', aggfunc='mean', fill_value=0)
return day_pivotdf = creating_feature(df)
pivot_df = create_pivot_table(df) ### 열 day , 행 hour 인 형태
위의 데이터는 일자별 시간 데이터로 1분단위의 데이터를 hour 단위의 평균을 내서 pivot table로 만든 것으로 해당 데이터프레임을 이번 실습에서 사용하였다.
pivot_df.plot(figsize=(7,3),color='blue',alpha=0.1,legend=False);
결과를 보면 위와 같이 일자별로 여러가지 경우가 있는 것을 볼 수 있다.
GMM을 사용하면 위와 같이 여러 시간별 데이터를 확률에 따라 여러개의 클러스터로 나눠준다.
## GMM
## GMM에서 AIC 기반 최적 cluster 갯수 찾음
def sel_cluster_number(day_pivot):
### 계산 시 필요한 형태가 일자별로 시간데이터로 그륩을 어떻게 정할 수 있을지이므로 -> 행 : day / 열 :hour (0~23시) 에 따라서 해당 행(일자) 한개가 어떤 클러스터로 분류될지 문제
X=day_pivot.T
lowest_aic = np.infty
lowest_bic = np.infty
best_n_components_aic = None
best_n_components_bic = None
n_components_range = range(1, 10)
for n_components in n_components_range:
# GMM 모델 생성
gmm = GaussianMixture(n_components=n_components, covariance_type='full')
gmm.fit(X)
# AIC 계산
aic = gmm.aic(X)
if aic < lowest_aic:
lowest_aic = aic
best_n_components_aic = n_components
# BIC 계산
bic = gmm.bic(X)
if bic < lowest_bic:
lowest_bic = bic
best_n_components_bic = n_components
print("최적의 n_components (AIC): ", best_n_components_aic)
print("최적의 n_components (BIC): ", best_n_components_bic)
return best_n_components_aic, best_n_components_bic
def run_gmm_cluster(day_pivot,n_components):
X=day_pivot.T
# GMM 모델 생성
### 행 기준으로 분류를 수행함.
### ex) 2018-07-01 / 2018-07-02 일자의 hour의 데이터가 각각 어떤 패턴에 들어가는 지 확인하고 싶다면,
### 위와 같이 index 가 일자별 / colums이 hour에 대한 값이여야함. 하나의 행의 데이터를 보고 이 패턴이 어느 패턴에 들어가는 지 표시함
gmm = GaussianMixture(n_components=n_components)
# 모델 학습
gmm.fit(X)
# 클러스터 할당
labels = gmm.predict(X)
# 클러스터링 결과 출력
Cluster_arr = []
for i in range(n_components):
print("Cluster ", i+1)
Cluster_arr.append(X[labels == i].T)
cluster_score = gmm.score(Cluster_arr[i].T)
print("Log-likelihood Score: ", cluster_score)
return Cluster_arr## gmm 적용
best_n_components_aic, best_n_components_bic=sel_cluster_number(pivot_df)
Cluster_arr=run_gmm_cluster(pivot_df, best_n_components_aic)
## 시각화
plot_gmm_cluster(Cluster_arr)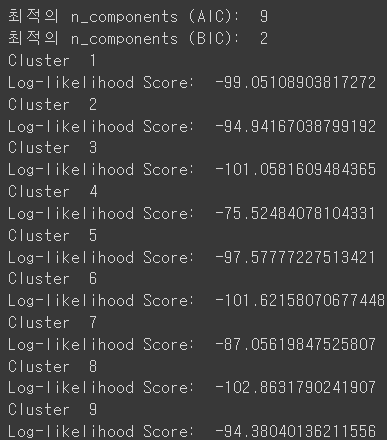
위의 결과를 보면 AIC 측면에서 최적의 클러스터는 9개로 결정되었고, 각각의 Log-likehood Score는 다음과 같다. Log-likehood는 모델의 파라미터를 구하는데 사용되는 최대 우도(Maximum Likelihood)를 로그 변환한 것으로
최대 우도는 주어진 데이터에서 모델의 파라미터를 조정하여, 그 데이터가 관찰될 확률을 최대화하는 파라미터 값을 찾는 과정이다. 앞에 (-)가 붙어있으므로 값이 작을수록 최대우도가 큰 것이다.
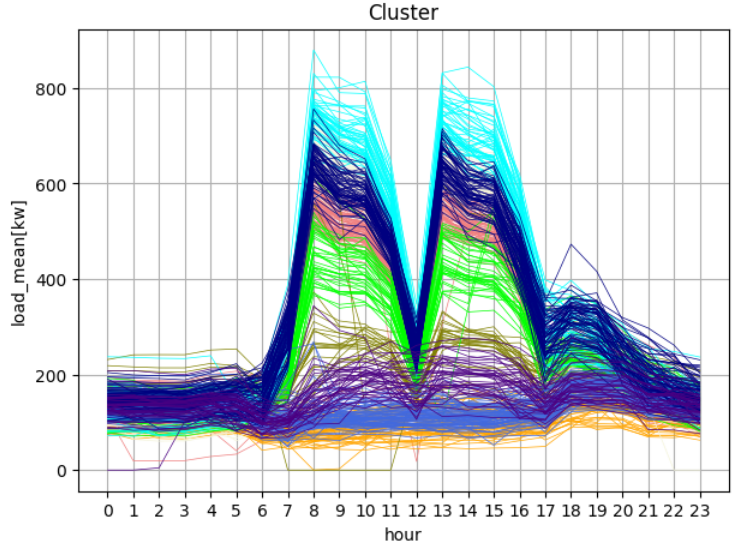
그전의 데이터를 9개의 클러스터로 나눠보면 위와같다.
그렇다면 클러스터당 월별로 어떻게 분포되어 있는 지를 확인하기 위해 클러스터당 월별 분포를 확인해 보았다.
def count_month_by_cluster(Cluster_arr,n_components):
cluster_merge_df = pd.DataFrame()
for i in range(n_components):
data=pd.DataFrame(Cluster_arr[i].columns)
data['year_day']= pd.to_datetime(data['year_day'])
data['month'] = data['year_day'].dt.month
data['day'] = data['year_day'].dt.day
data['cluster'] = i
cluster_merge_df = pd.concat([cluster_merge_df, data], axis=0, ignore_index=True)
group = cluster_merge_df.groupby(['cluster','month'], as_index=False).agg(
count_cluster = ('cluster', 'count')
)
fig, axes = plt.subplots(nrows=len(group['cluster'].unique()))
plt.subplots_adjust(hspace=1.2)
fig.set_size_inches(10,17)
for val in group['cluster'].unique():
ax= axes[val]
sns.barplot(x='month', y='count_cluster', data=group.loc[group['cluster']==val], ax=ax)
ax.set(
title=f'{val+1}th Cluster',
yticks=[0,5,10,15,20,25,30],
ylabel='count'
)
ax.grid()### 월별 클러스터 분포도
count_month_by_cluster(Cluster_arr,best_n_components_aic)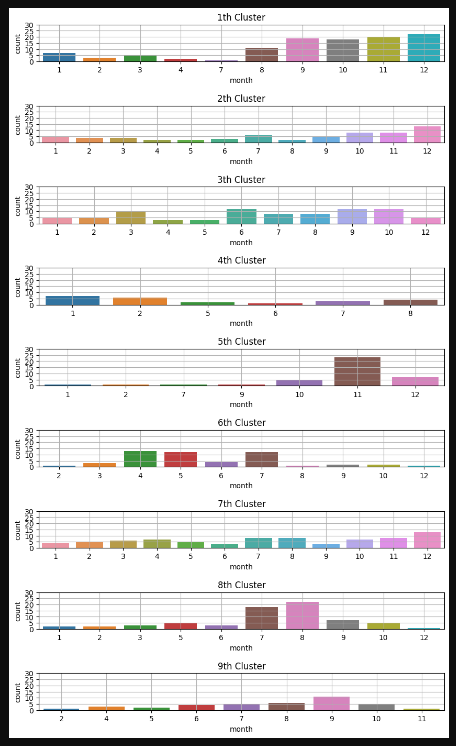
클러스터별 월별 분포를 보면 어떤 클러스터는 월별 분포가 두드러진 것도 있고 어떤 것은 월마다 큰 편차가 없어 구분하기 어려운 것도 있다.
위의 데이터는 시간에 대한 값으로 클러스터를 분류한 것으로, 크기에 대해 민감하다. 그러나 패턴을 감지하려면 시간에 따른 크기보다 시간의 변화량에 대한 값으로 클러스터를 분류하는 것이 효과적인 것 같다.
따라서 아래와 같이 시간의 변화량으로 변환하여 위의 과정을 다시 진행하였다.
### GMM - 시간대별 퍙균변화량 CLUSTER 에 따른 분류 방법
df = creating_feature(df)
pivot_df = create_pivot_table(df) ### 열 day , 행 hour 인 형태
pivot_df_diff=pivot_df.diff(1).fillna(0)
### data 형태 보기
pivot_df_diff.plot(figsize=(7,3),color='blue',alpha=0.1,legend=False);
## gmm 적용
best_n_components_aic, best_n_components_bic=sel_cluster_number(pivot_df_diff)
Cluster_arr=run_gmm_cluster(pivot_df_diff, best_n_components_aic)
## 시각화
plot_gmm_cluster(Cluster_arr)

### 월별 클러스터 분포도
count_month_by_cluster(Cluster_arr,best_n_components_aic)
우선 시간의 변화량의 데이터를 가지고 클러스터링 한 것을 가지고 추후에 데이터 이상치 탐지 모델에 사용할 예정이다.
### 클러스터별 그래프에 표시해 시각화할 수 있다.
### 클러스터별 index (일자) 저장
cluster_index = []
for i in range(len(Cluster_arr)):
temp_index=Cluster_arr[i].T.index
cluster_index.append(temp_index)
fig,axes=plt.subplots(nrows=len(cluster_index))
fig.set_size_inches(10,16)
plt.subplots_adjust(hspace=1.1)
for idx , sel_index in enumerate(cluster_index):
ax = axes[idx]
sns.lineplot(x=df['Date'], y='load', data=df, ax=ax, errorbar=None)
x_coord = sel_index ##### cluster 별 날짜
y_coord_arr = []
for day in x_coord:
y_coord = df.loc[df['year_day']==day, 'load'].max() ### 해당 날짜에 해당 하는 값중 가장 큰 값
y_coord_arr.append(y_coord) ## 날짜의 수에 해당하는 load 값의 최대치를 저장한다. ( 하루중 가장 큰값)
ax.set(title=f'{idx+1} Cluster')
ax.scatter(x_coord, y_coord_arr, marker='*', s=30, color='red')
ax.tick_params(axis='x',labelrotation=0)
'시계열분석_python' 카테고리의 다른 글
| [SARIMAX]전력데이터 분석 ( ARIMA + Fourier 계절성 ) (0) | 2023.04.02 |
|---|---|
| [LSTNET]빌딩 전력 수요예측 (Functional 방법) (0) | 2023.03.26 |
| [LSTNET] 빌딩전력예측 딥러닝 (0) | 2023.03.26 |
| [SARIMA]빌딩 전력 시계열 모델 예측 (0) | 2023.03.23 |
| [서평이벤트 당첨_이지스퍼블리싱] 점프투 파이썬_라이브러리 예제편 (0) | 2022.05.27 |





